このコラムは、Voicyをテキスト化し一部抜粋したものです。
今回は、大手物流宅配事業デジタル本部にてビッグデータと向き合う、寺﨑さんにインタビューした記事です。
質問です。
Q,アイスクリームを食べる人が増えると、
熱中症患者も増えるのでしょうか!?
その原因をあらゆる角度から考察していくのが統計学です。今回は寺﨑さんが語る統計学へのアプローチを、一緒に考えていきたいと思います。
質問の答えは、下記レポートにて!
1.統計学との出会い
私はもともと数学が好きでした。
国語のように曖昧な答え方をしないといけないものよりも、答えが明確化している方がすごく好きだったからです。数学の答えはひとつと決まっていますが、アプローチ方法は様々です。答えに向かって考えることがこれほど楽しいものなのかと、数学から教わりました。
学生の頃は先生を目指し、中学と高校の数学教員免許を取得しました。教育実習では中学校一年生に対して、1÷0と0÷1の違いを教えたのが人生初の授業でした。簡単な事ですが「どうしてこの答えになるのかな?」と考えることがとても面白かったです。さらに単なる数学というよりも、世の中で起こっている現象を考えることが数学の魅力のひとつだと思います。
数学の世界に魅了されているうち、それまで学校で学んだ知識の中で教壇に立つのは、果たしてどうなのか?と自分の中で思うところがあり、教員の道ではなく一般企業へ就職しました。社会の中で数学の活用方法を知ると、更に面白い世界が広がっていることに気が付きました。
社会人となってからは設計部門へ配属されました。これまで学生時代に一生懸命勉強していた数学が、世の中で活かされている場面に遭遇し、ますます興味が湧いてきました。クライアント様の課題に対し、解決に向けたアプローチを検討する中で、統計が必要になってくることが多々ありました。実際に数学を使う現場を体験してみて、点と点が線でつながったときに、更に仕事が楽しくなってきました。統計に関する勉強方法は、書物を頭に叩き込んで知識を増やすよりも、現場で経験しながら学ぶ方が興味も理解も深まる様に思います。

2.統計の活用方法
統計は現象を調査し、正しく把握し活用します。そのため、数字に翻弄されてしまわぬように気をつける必要があります。数字だけでは比べられないものを比較する時に統計は役立ちます。
ある国に友達がいて、その人と自分の所得を比較したとします。所得はこちらの方が高いけれど、生活水準は友人の方が高く裕福な生活をしていた場合、単純に所得の金額だけでは比較できません。全体の中で所得や生活水準がどこに位置するのか、客観的な視点で比較しなければ正しい把握はできません。
また、平均年収を例にすると高所得の方々が平均値を上げている事もありますが、平均値で見るのか、中央値で見るのか、見方によって随分変わりますので、自分の年収を正しく把握するにはどの視点で見ればよいか考えることも大切です。
統計を活用する中で気を付けたい点は、ニュースなどで報道されている数字を切り取って鵜呑みにしないようにしてほしいです。例えばコロナの陽性率に関してですが、パーセンテージだけを提示されて、判断すると誤解を招くこともあります。PCR検査の母数や、検査の正確性などを踏まえて、確率を含めて判断する必要があると思います。

私は、仕事柄荷物のデータを扱います。時系列で荷物の個数の変化を見る場合、前年同日比較、前年同週同曜日の比較を良く行いますが、傾向を見る時は、週を比較すると傾向が一致しやすいです。見せ方によって判断が変わってくる場合がありますので、現状をいち早く把握しグラフを可視化し、統計的な数字を出す必要が出てきます。
学生時代は問題に対して正解が出せました。
しかし社会に出て統計を使ってみると、何を見たいかによって使う統計の知識が変わります。その物差しは経験が影響するところが大きいと思います。
★冒頭の質問★
『アイスクリームを食べる人が増えると、熱中症患者が増えるのか?』
これは一見すると熱中症が原因ではないかと推測されがちですが、実際はどうなのか考える必要があります。
正解は、『単純に暑い日が増えるから、アイスを食べる人が増える』です。
実際の原因は気温の上昇と考えられるのですが、見えている数字だけで因果関係を判断するのは良くないという例でした。
3.統計の学び方
実は私、高校の時の統計学の教科書『確率と統計と』を、今でも愛読しています。日ごろから教科書を見直し、どういう時に統計を用いるのがベストかと常に頭に置くことを日課にしています。また統計検定2級を取得しており、検定試験の内容で統計の基礎は十分学べると思います。
統計で難しい公式が出てきますが、公式は検索すればすぐわかりますので、公式を覚えることはさほど重要ではありません。それよりもむしろ、何を使うと、何ができて、どういう数字を表現できるのか、という点を押さえておくことがポイントだと思います。
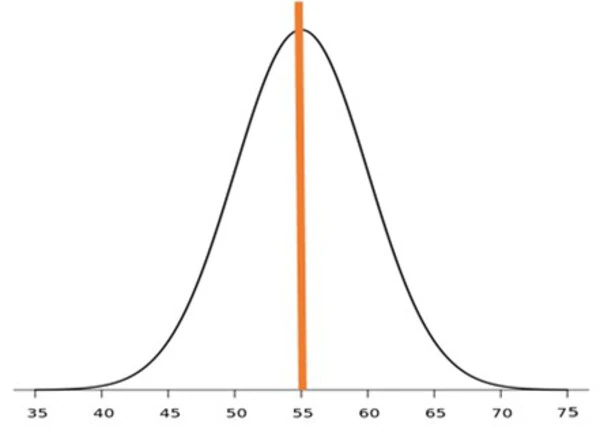
正規分布のわかりやすい例として、偏差値を考えてみます。
下の図は、偏差値の正規分布のグラフです。
正規分布では、平均を中央に置きます。オレンジの線は平均軸になります。その平均軸に対し、左右対称の形をしているのが特徴です。実は偏差値は、数字だけを切り取って一喜一憂しても意味はありません。そのテストを受験した人数によって偏差値は変わるからです。
見るべき点は、【全体の中で、自分がいる位置がどこであるか】です。これを把握しておくことが正しい偏差値を知る方法です。
4.第三次ITブームとビッグデータ
ITブームはこれまでに3回ありました。
-
第一次ITブーム:1950年代コンピュータが出来始めたことによる
-
第二次ITブーム:1980年代コンピュータが一般家庭に普及し始めたことによる
-
第三次ITブーム:2000年前後から昨今インターネットの普及による膨大なデータ蓄積と、コンピュータデバイスの爆発的な性能向上・小型化、クラウドの普及による
現在は、第三次ITブームを迎えています。この背景には、ビッグデータを活用できる環境や体制が整ったことが要因であると考えています。
私は、ビッグデータを扱う仕事をしていますが、『本来求める数字は何か?』ということを意識しながら業務を行っています。他の数字に埋もれて正確な情報を見失ってしまう恐れがあるためです。そのため、数字の精査は入念に行っています。
ビッグデータはもともと、どこにでも存在しているものでした。データとして今まで対象ではなかったものも、第三次ITブームの到来により大量に処理できるようになりました。
このことにより、データそのものが見直されています。例えば、単なるログとして存在していたデータ(機械のログデータ、解析ログデータなど)を集めることによって、以前は勘と経験で行っていたことが、裏付けと予測ができるようになりました。今後、更にデータの価値を見出すことで、ビッグデータの需要は拡大して行くと思います。
5.最後に
身近なところから、数字に興味を持っていただくことが統計学を学ぶスタートだと思います。ただし、情報を正しく読み取れるかどうかは、あなた次第です。
決して数字に踊らされることなく、正しい判断ができるよう経験を磨き、ビジネスにつなげていけるように、日ごろから統計学としての目線を身につけてください。